Baroclinic Momentum Equations¶
Baroclinic Momentum Equations¶
The baroclinic momentum equations are the stacked shallow water equations:
The timestepping for these equations is a (quasi?) second-order Runge-Kutta step for the inertial oscillations and a forward-backward Euler step for the pressure (gravity) waves. Using the graphical notation from [59], it looks like:
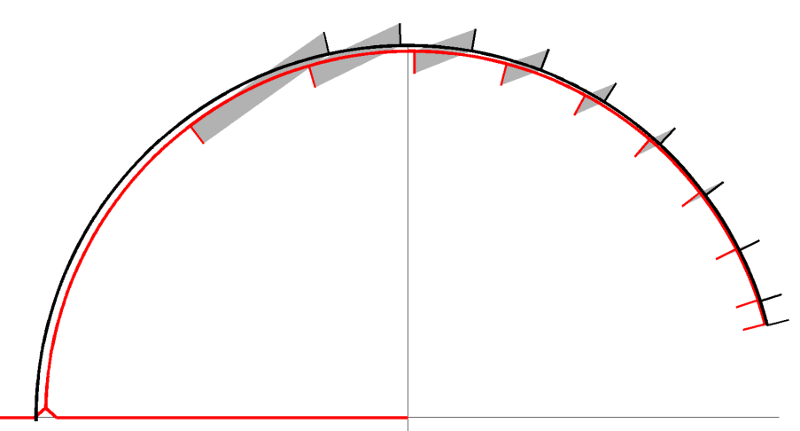
Graphical notation for timestepping schemes in which the black line represents the ideal solution and the red line shows the actual solution. Phase errors are represented by the grey shapes between the bars normal to the circle.¶
The timestep used in ROMS looks instead like:
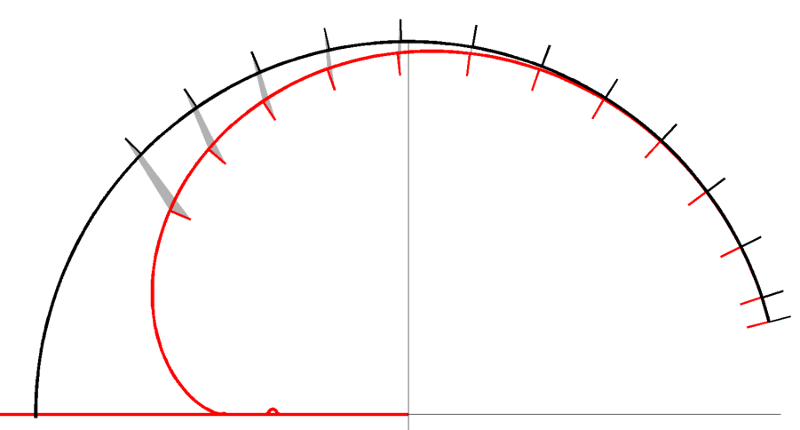
Graphical notation for the Adams-Bashforth technique used in the ROMS model.¶
The ROMS timestepping has smaller phase errors, strong damping at high frequency. The MOM6 use as a global climate model has made the phase errors of lower priority. However, the phase errors may become more problematic for future uses of MOM6. While the MOM6 use of the ALE remapping makes an Adams-Bashforth scheme impractical, there may be a better timestepping scheme out there for MOM6. Please let the MOM6 developers know if you would like to work on this problem.